- Death counts
- Census counts
For years 1751-1860, data in 5-year age groups (except for the youngest and oldest ages) were split into single-year age groups using a method of linear interpolation applied to logarithms of the raw data. For death counts during this period, the given age intervals were usually 0, 1-2, 3-4, 5-9, 10-14, ... , 85-89, and 90+. For some years, however, raw data above age 90 were available in greater detail: 90-94, 95-99, and 100+. In all situations, we used the greatest level of detail available in the raw data.
Before interpolating, the raw data were scaled by dividing the death counts by the length of the age interval (the 90+ and 100+ category were divided, arbitrarily, by 15 and 5 years, respectively). Thus, the resulting estimates are scaled to single-year age intervals. In applying the linear interpolation method, the midpoint of an age interval gives the x-coordinate, while the log of the scaled death count gives the y-coordinate.
Several additional notes are needed regarding this procedure. First, obviously, since raw data for age 0 were available, no estimate was obtained for this age. Second, however, we determined that it was not useful to include age 0 in the linear interpolation model to obtain estimates for age 1, since the number of deaths at age 0 is atypical. Instead, the estimate for age 1 is derived by a slight extrapolation, using the raw data for age groups 1-2 and 3-4. Third, in deriving estimates for ages 88-104, the x-coordinate for the open 90+ category was (arbitrarily) set equal to 95; technically, then, estimates for ages 88-94 were derived by interpolation, while those for 95-104 were derived by extrapolation. (When the open interval is 100+ rather than 90+, the x-coordinate was set equal to 102.5.) For obvious reasons, we do not have great confidence in the accuracy of these estimates at very high ages. At the same time, estimates at such high ages in this era do not matter much for such important indices as life expectancy at birth (from either a period or cohort perspective).
By this method of log-linear interpolation, we obtained initial estimates of death counts by age,
, where x refers to age at death (by single years). These estimates were multiplied by adjustment factors to take account of differences in cohort size, yielding a second set of estimates, 
. After the correction for relative cohort size, a further adjustment was made to ensure that the estimated death counts add up to the original total number of deaths in each age group, yielding 
. These values were the final estimates for all single-year ages except ages 1 and 2, which required a final ad hoc adjustment. These three successive modifications of 
are explained below.
First, consider the cohort size adjustment, which is applied to the initial estimates (derived using the log-linear interpolation method). We begin by assuming that the formula for this adjustment should contain the quantity
,
where the 
equals the mean of birth counts for the two cohorts whose members are age x at some time during the year in question, and 
equals the mean of the five values of in the associated 5-year age group. Thus, 
gives the average size of the two cohorts whose deaths may have occurred at age x in this year relative to the (weighted) average size of the six cohorts whose deaths may have occurred in the associated 5-year age group.
Now, suppose that all birth cohorts represented in these averages are of equal size. We call this scenario the "constant births" model. In this situation, would equal one, and 
should already be a good estimates of 
. If these birth cohorts are not of equal size, however, then we need to adjust . Relative to the constant births model, the error in the estimated death count equals 
(thus, the absolute error relative to our initial estimate). Analogously, the relative difference between the observed and its value in the constant births model equals 
. We might reasonably suspect that these two quantities would be closely related, and our empirical investigation confirms that their relationship can be expressed by a simple regression model:
.
Furthermore, our empirical analyses have shown that 
in the equation is very close to zero and can thus be ignored. As shown in Table 1, the slope 
is close to one for years 1861-1900, which is the most relevant period for our purposes. Therefore, we can conclude that
,
and thus let 
, which completes the adjustment of the estimated death counts for differences in cohort size.
After making this cohort size adjustment, the values of 
need to be adjusted further to ensure that the estimates add up to the original totals for the age groups of the raw data. For example, if 
, then
.
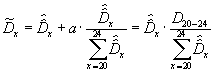Finally, a small inadequacy in the interpolation method affecting the results for ages 1 and 2 was noted. The estimated number of deaths for age 1 was consistently too low, while the opposite occurred for age 2. An ad hoc correction procedure was developed based on an analysis of more detailed data for years 1861-1890 and then applied to the results for all earlier years. We first computed the average error in the estimated deaths for age 1 relative to the total number of deaths for ages 1-2. This quantity was fairly constant during the period 1861-1890 (rising noticeably thereafter), and thus we computed its average over these years alone:
,
where 
and 
are the actual deaths for age 1 and 2, respectively, and 
is the current estimate of the death count for age 1. Thus, for females, and 
need to be adjusted in opposite directions by an amount equal to 0.0311 times the total number of deaths for ages 1-2, which is known even during the period 1751-1860:
and
.
where 
and 
are the final estimates of death counts for ages 1 and 2. For males, the adjustment is made using a correction factor of 0.0326.
Population data during 1751-1860, based on census counts at 5-year intervals, were available only in 5-year age groups (0-4, 5-9, 10-14, ... , 85-89, 90+). These numbers were split into single-year age groups by nearly the same method used for the death counts. In fact, it was easier to apply the procedure in this case, since the available age groups were more regular over age and time.
First, initial estimates, 
, were obtained by log-linear interpolation. Second, these estimates were adjusted by the formula
.
Note that the cohort size adjustment factor, 
, is slightly different than 
in the previous case. Here,
where 
equals the birth count of the cohort that is aged x to x+1 at the time of the census (which occurs on December 31 of the census year), and 
equals the mean of the five values of 
in the associated 5-year age group. Third, this set of estimates was adjusted further to ensure that totals within 5-year age groups add up to their original values (see method described earlier for the deaths). For the census estimates, there was no need to make a final adjustment for the age group 1-2.
After splitting 5-year death data for years 1751-1860 into single-year age groups, we then split single-year death data for years 1751-1900 into Lexis triangles using a linear regression model. For years 1901-1991, raw data by individual triangles were available at all ages, and these data were then used to derive the model that was subsequently applied for splitting the single-year data for earlier years.
Many linear models were fit to the raw triangle data for 1901-1991, and seven of these models are summarized in Tables 2a (females) and 2b (males). In all cases, the dependent variable in these models was the proportion of deaths in each 1x1 Lexis square contained in the lower (right-hand) triangle of that square. All models were fit by weighted least squares, where the weights were proportional to the number of deaths in the entire Lexis square.
All of the coefficients in the most comprehensive model, Model VII, are statistically significant at the 0.001 level. Thus, all the terms included in these models have some descriptive value. The age pattern of variation in the proportion of lower-triangle deaths (higher than average in the earliest and latest years of life) is easily visible from an inspection of the age coefficients for Models I-IV. For the more complicated models, it is necessary to combine the effects of the interaction terms with the age coefficients in order to observe this same age pattern. Note: These linear models were fit using both single-year age groups (0-104) and 5-year age groups (only the latter are shown in Tables 2a and 2b). For all computational purposes, we used the models with single-year coefficients. The models with 5-year coefficients are used for presentation purposes only, although in fact they produce only slightly inferior results if used for computation as well.
The next variable in these models is labeled "birth proportion," which is the number of births in the younger cohort (corresponding to the lower triangle of the Lexis square) as a proportion of the total births in the two cohorts that traverse the Lexis square in question. As such, this variable is analogous to the "death proportion," which is the dependent variable in these models. Therefore, a positive coefficient is a reasonable result.
The death proportions tend to increase over the observation period, as reflected in the positive coefficient for the variable "year" in Models IV through VII. This increase is much stronger for age 0, as seen in the interaction term. A curious result, however, is that the rapid increase in the death proportion for age 0 reverses itself around 1965. This change is captured in the next set of interaction terms and can be observed graphically in Figures 1a. A final pair of coefficients is included in order to reflect the impact of the Spanish flu epidemic during the winter of 1918-19. The increase in the death rate during that winter greatly elevated the proportion of deaths in lower triangles for 1918 (dominated by months at the end of the year) and in upper triangles for 1919 (dominated by months at the beginning of the year).
Having fit these seven models, we may be tempted to extrapolate the proportion of lower triangle deaths using the best-fitting model, Model VII, into the earlier time periods (1751-1900). An obvious problem with this approach is well illustrated in Figures 1a, 1b, and 1c, since the predictions outside of the observation period quickly become implausible. Especially for age 0, but for other ages as well, it does not seem believable that the proportion of lower-triangle deaths in earlier time periods could have been substantially below 0.5, as predicted by an extrapolation of Model VII.
A visual inspection of the raw data in the earliest portion of the observation period, 1901-1910, seems to show no trend over time, especially for age 0 (which is less affected by random variation because of the large number of deaths). This result suggests that the levels of these death proportions may not have increased substantially in earlier years. Therefore, we chose to derive a predicted proportion of lower triangle deaths for years 1751-1900 using Model VII but holding the value of the year variable constant at 1910. This assumption eliminates the implausible time trend for years before 1900 and yields predictions of the level of the death proportion that are similar to those observed in 1901-1910. These predictions still include the effect of variations in the birth proportion variable when available. Note: Birth counts were available back to 1749 only. For earlier cohorts, we set the birth proportion variable equal to 0.5. Thus, at advanced ages, the predicted proportion of lower-triangle deaths was constant prior to some time period.
The method employed for splitting data from 5-year age groups into single-year age groups was the third of three methods that we tested for this purpose. We refer to the final method as "log-linear," since it consists of a linear interpolation applied to logarithms of the raw data. The other two methods are called "linear" and "spline." The linear methods differs from the log-linear only in the fact that it does not employ logarithms: in other words, a linear interpolation is applied directly to the raw data. The spline method is also applied to the raw data (without logarithms). Instead of a simple linear interpolation, however, it involves a more complicated method of fitting moving sequences of cubic splines to raw death (or census) counts. After various comparisons, we determined that the log-linear method was, in general, at least as accurate (in some cases, more accurate) than the other two methods. It also has a clear advantage of simplicity compared with the spline method.
Unfortunately, it was not possible to use the same method for the two steps in the total splitting process. In other words, our best method for splitting data from 5-year to single-year age groups is fundamentally different from our method for splitting single-year age groups into Lexis triangles. Of course, this distinction matters only for the death counts. Obviously, all of the variants of the interpolation method have the advantage of simplicity compared to the linear regression model, and we would have preferred to apply one of these methods (in particular, the log-linear interpolation method) also for splitting single-year data into Lexis triangles. The interpolation methods failed in this case, however, and we were forced to employ a more complicated strategy involving a linear regression model. Briefly, the reason that the simpler interpolation methods do not work for this purpose is that the pattern of death counts by Lexis triangle is affected not only by age, but also by the seasonality of mortality (since upper-triangle deaths are weighted disproportionately toward the more lethal winter months).