| Intercensal Survival |
| Topics: |
| I. | Introduction |
Suppose that a country conducts censuses every 5 years on January 1. Then, population estimates by single years of age are available at 5-year intervals, but no comparable estimates are available for intervening years. Intercensal survival methods provide a simple and reasonable means of estimating the population by age on January 1 of every year during the intercensal period.
A Lexis diagram to represent this situation is shown below in Figure 1. The cohort aged x at time t is followed through time for 5 years. Suppose that deaths for the population are recorded with a relatively high level of detail; i.e., for each year in this intercensal period, death counts are available by both age and year of birth. Thus, it is known with some precision how many lifelines ended by death in each of the small triangles, called "Lexis triangles," shown in Figure 1.
Figure 1
Intercensal survival (in general)
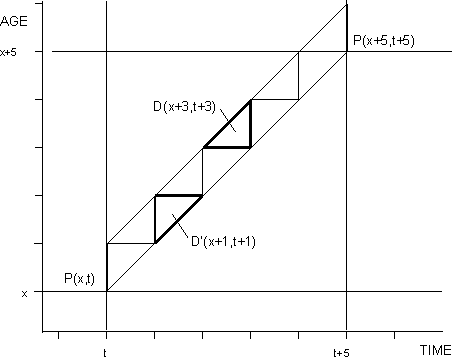
The information represented by Figure 1 can be used to estimate the size of the cohort on January 1 of each of the intercensal years. The simplest procedure would consist merely of subtracting death counts for the cohort from the initial census count to obtain population estimates for each succeeding year. Unfortunately, the final step of such a computation usually yields an estimate of cohort size at time t + 5 that differs from the amount given by the corresponding census. This inconsistency is caused by two factors: migration and error. Although both of these factors tend to be small relative to the cohort size (at least for national populations), they should not be ignored.
| II. | Intercensal Population Estimation |
We present the intercensal population estimation in general. Subsequently, we give two possible adjustment methods to correct for the migration/error inconsistency:
The population estimates found on the Berkeley Mortality Database use the latter method when we have migration estimates.
In both the standard method and the method using migration estimates, two types of cohort need to be addressed separately when obtaining population estimates: nonbirth cohorts and birth cohorts (those cohorts that are born during the intercensal period).
Nonbirth cohorts are those cohorts in the intercensal period that are already alive at the time of the first census. Figure 1 shows the age-x cohort–the youngest of the nonbirth cohorts. All cohorts above this are also nonbirth cohorts, and all below are birth cohorts. Consider the following framework for population estimation in nonbirth cohorts.
| Let P(x, t) | = census count for those x years old at time t (i.e., on January 1 of year t); x = 0, 1, . . . . |
| D(x, t) | = number of "lower-triangle" deaths among those x years old in year t. |
| D'(x, t) | = number of "upper-triangle" deaths among those x years old in year t. |
Then, assuming no migration or error,
P(x, t) = ![]()
![]()
![]() [D'(x + i, t + i) + D(x
+ i + 1, t + i)],
[D'(x + i, t + i) + D(x
+ i + 1, t + i)],
or, if we know the size of a cohort at time t, we can estimate its size at the time of the next census, t + 5:
P*(x + 5, t + 5) = P(x,
t) – ![]()
![]()
![]() [D'(x + i,
t + i) + D(x + i + 1, t + i)].
[D'(x + i,
t + i) + D(x + i + 1, t + i)].
If there is migration or error, then this estimate will differ from the actual
count, P(x + 5, t + 5), at the time of
the next census. By definition, total error and migration are equal to the observed cohort
size at the second census minus its estimated size, P*(x + 5, t + 5).
We will refer to this difference as ![]() x:
x:
![]() x = P(x + 5, t + 5) – P*(x
+ 5, t + 5).
x = P(x + 5, t + 5) – P*(x
+ 5, t + 5).
The final step in obtaining intercensal population estimates for the cohort is to
redistribute ![]() x yearly throughout the intercensal period, weighting
it via weighting functions wi, i = 0, . . ., 4,
where
x yearly throughout the intercensal period, weighting
it via weighting functions wi, i = 0, . . ., 4,
where ![]()
![]()
![]() wi(
wi(![]() x) =
x) = ![]() x.
(The choice of weighting functions is discussed in Adjustment
Methods, below.) We thus arrive at intercensal population estimates for every year
x.
(The choice of weighting functions is discussed in Adjustment
Methods, below.) We thus arrive at intercensal population estimates for every year
Intercensal Population Estimate for Nonbirth Cohorts P(x + n, t + n) = P(x, t) – |
If we set n equal to 5 in the above equation, we get the population count from the second census.
Birth cohorts are those cohorts that begin during the intercensal period. Figure 2 below shows an example of a birth cohort. Birth cohorts differ from nonbirth cohorts in their shape within a Lexis diagram: birth cohorts are not parallelograms due to their first year, and they span a shorter length of time during the intercensal period. However, population estimates are achieved similarly after these differences are taken into account.
Initial population estimates are obtained by subtracting the number of deaths at each year from the number of births for the cohort. For the cohort born during year t + j – 1, j = 1, . . ., 5, in the intercensal interval [t, t + 5):
| Let K | = length of the interval [t + j, t + 5) |
| = age (at last birthday) of cohort born during year t + j – 1 at the time of the second census | |
| = 5 – j. | |
| Let Bt+j–1 | = number of births during year t + j – 1, i.e., during the interval [t + j – 1, t + j) . |
An initial estimate of population size for the cohort born in year j at the time of the second census is
P*(K, t + 5) = Bt+j–1
– D(0, t + j) – ![]()
![]()
![]() [D'(
i – 1, t + j + i) + D( i, t
+ j + i)],
[D'(
i – 1, t + j + i) + D( i, t
+ j + i)],
and the difference between this estimate and the actual population count is then
![]() -j = P(K, t + 5) – P*(K,
t + 5).
-j = P(K, t + 5) – P*(K,
t + 5).
The "-j" in the above expression is simply to keep the consistency with the previous notation; the subscript serves to identify the age of the cohort at the time of the first census. Since these are birth cohorts, they have negative age at the first the time of the first census.
As before, we obtain the standard estimate of population size (on January 1)
for this birth cohort at ages k = 0, . . . , K
by redistributing ![]() -j via weighting functions, vi,K,
throughout the intercensal period:
-j via weighting functions, vi,K,
throughout the intercensal period:
Intercensal Population Estimate for Birth Cohorts P(k, t + j + k) = Bt+j–1
– D(0, j) – |
These weights are defined below.
| III. | Adjustment Methods |
The population estimate formulas derived in Intercensal Population Estimation above are completed by the choice of the weighting functions used to distribute the migration/error throughout the intercensal period. Below are two methods for choosing the weighting functions.
The standard methods weight the total error/migration, ![]() x,
uniformly throughout the intercensal period. Though we have been using a 5-year
intercensal period to be concrete, consider now an intercensal period of L years.
Then, for nonbirth cohorts, the standard estimate of population size during intermediate
years is:
x,
uniformly throughout the intercensal period. Though we have been using a 5-year
intercensal period to be concrete, consider now an intercensal period of L years.
Then, for nonbirth cohorts, the standard estimate of population size during intermediate
years is:
Standard Weighting Functions for Nonbirth Cohorts wi( |
For birth cohorts, we likewise distribute the total error/migration uniformly thoughout
the intercensal period. However, the interval amount of time over which to distribute
varies for each birth cohort. Recall that the length of the interval for the birth cohort
born during year t + j – 1 is K = L
– j, where, before, we were using L = 5. To distribute ![]() -j
uniformly, we use the following weights:
-j
uniformly, we use the following weights:
Standard Weighting Functions for Birth Cohorts v0,K( |
![]() The Method Using Migration Estimates
The Method Using Migration Estimates
If total net migration estimates mi are known for the population for every year of the intercensal period, we can take this information to redistribute the total error/migration based on the pattern of migration. Basically, we would like the distribution to match the migration trend; if migration is positive and large one year, we want the portion of the total error/migration to be large that year relative to the other years. If migration is negative one year, then we want to match with an appropriately scaled weight of the total error/migration. This leads us to the following weighting functions for nonbirth cohorts:
Method of Migration Weighting Functions for Nonbirth Cohorts wi( |
Weighting under this method is complicated only due to the fact that we do not know ahead of time whether the total error/migration for a cohort matches in sign to the average migration over the intercensal period . The weighting functions above sacrifice simplicity to overcome this obstacle.
Since migration is typically concentrated in ages around 20-40 years, this method is only applied to nonbirth cohorts. For birth cohorts, the standard method of weighting is used.
| IV. | Example |
The following is an example of applying the standard method of estimation to an intercensal birth cohort.
Say that there are censuses at exact times t and t + 5 and that j = 2. Then K = 2, since the cohort born in year [t + 2, t + 3) will be age 2 (last birthday) by the time of the second census. This gives us the Lexis diagram in Figure 2.Figure 2
Intercensal survival (for new cohorts)
Population estimates for the cohort born in year in year
[t + 2, t + 3) for January 1 of each year from birth until the second census are given below:
P(0, t + 3) = Bt+2 – D(0, t + 2) +·
-3,t
P(1, t + 4) = Bt+2 – D(0, t + 2) – [D'(0, t + 3) + D(1, t + 3)] +
·
-3,t
P(2, t + 5) = Bt+2 – D(0, t + 2) –
[D'(i – 1, t + 2 + i) + D(i, t + 2 + i)] +
-3,t
Note: P(2, t + 5) equals the census total for 2 year olds at the second census.
| V. | Further Adjustments – Intrayear Censuses
[under construction] |
The arguments above make the explicit assumption that the two censuses that bound the intercensal period each occur on January 1 of its respective year. Often, though, this is not the case. (In Japan, for example, most censuses have occurred in October.) Care needs to be taken to account for intrayear censuses in obtaining intercensal population estimates. Consider Figure 3 below depicting an intercensal period bounded by two intrayear censuses. The inset in Figure 3 is a magnified view of the first two triangles of the highlighted cohort.
[Insert Figure 3 here.]
The first assumption we make is that the deaths in the triangles depicted in the inset
are distributed uniformly throughout the year. The net result, then, is to do the method
of intercensal survival except that, for each cohort, the death counts of the end
triangles are multiplied by the fraction of area that is within the intercensal period.
For the triangles depicted in the inset of Figure 3, we would count for the shaded region ![]() (1 – f1)2 · D'(x,
t) + (1 –
(1 – f1)2 · D'(x,
t) + (1 – ![]() f12) · D'(x
+ 1, t), where f1 is the fraction of the year in year t
that the first census was conducted.
f12) · D'(x
+ 1, t), where f1 is the fraction of the year in year t
that the first census was conducted.
The second assumption we make is that the census population size estimate at each age of the census is distributed uniformly throughout the age. Then P(x + f1, t + f1) = (1 – f1) · P(x, t + f1) + f1 · P(x + 1, t + f1).
With these two assumptions, we can proceed with the method of intercensal survival to obtain population estimates for each whole year in the intercensal period. . . .
Maintained by: Pierre Vachon